综合示例

QAOA

QAOA 是众所周知的量子经典混合算法。 对于n对象的MAX-CUT问题，需要n个量子位来对结果进行编码，其中测量结果（二进制串）表示问题的切割配置。

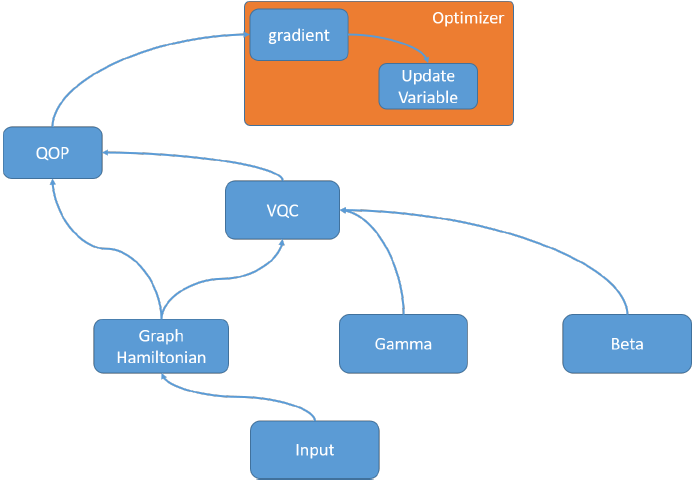
我们通过 VQNet 可以有效地实现 MAX-CUT 问题的 QAOA 算法。 VQNet中QAOA的流程图如下所示。

我们给定一个MAX-CUT的问题如下

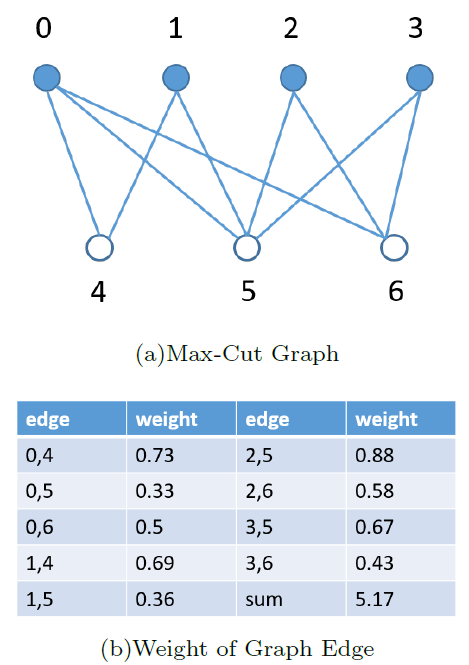
首先，我们输入 MAX-CUT 问题的图形信息，并构造相应的问题哈密顿量。

PauliOperator getHamiltonian()
{
    PauliOperator::PauliMap pauli_map{
        {"Z0 Z4", 0.73},{"Z2 Z5", 0.88},
        {"Z0 Z5", 0.33},{"Z2 Z6", 0.58},
        {"Z0 Z6", 0.50},{"Z3 Z5", 0.67},
        {"Z1 Z4", 0.69},{"Z3 Z6", 0.43},
        {"Z1 Z5", 0.36}
    };

    return PauliOperator(pauli_map);
}

然后，使用哈密顿量和待优化的变量参数x，构建 QAOA 的vqc。 QOP 的输入参数是问题哈密顿量、VQC 、一组量子比特和量子运行环境。QOP 的输出是问题哈密顿量的期望。 在这个问题中，损失函数是问题哈密顿量的期望，因此需要最小化 QOP 的输出。 我们通过使用梯度下降优化器 MomentumOptimizer 来优化vqc中的变量x。

#include "QPanda.h"
#include "Operator/PauliOperator.h"
#include "Variational/var.h"
#include "Variational/expression.h"
#include "Variational/utils.h"
#include "Variational/Optimizer.h"
#include <fstream>

using namespace std;
using namespace QPanda;
using namespace QPanda::Variational;

VQC parity_check_circuit(QVec &qubit_vec)
{
    VQC circuit;
    for (auto i = 0; i < qubit_vec.size() - 1; i++)
    {
        circuit.insert( VQG_CNOT(
            qubit_vec[i],
            qubit_vec[qubit_vec.size() - 1]));
    }

    return circuit;
}

VQC simulateZTerm(
    QVec &qubit_vec,
    var coef,
    var t)
{
    VQC circuit;
    if (0 == qubit_vec.size())
    {
        return circuit;
    }
    else if (1 == qubit_vec.size())
    {
        circuit.insert(VQG_RZ(qubit_vec[0], coef * t*-1));
    }
    else
    {
        circuit.insert(parity_check_circuit(qubit_vec));
        circuit.insert(VQG_RZ(qubit_vec[qubit_vec.size() - 1], coef * t*-1));
        circuit.insert(parity_check_circuit(qubit_vec));
    }

    return circuit;
}

VQC simulatePauliZHamiltonian(
    QVec& qubit_vec,
    const QPanda::QHamiltonian & hamiltonian,
    var t)
{
    VQC circuit;

    for (auto j = 0; j < hamiltonian.size(); j++)
    {
        QVec tmp_vec;
        auto item = hamiltonian[j];
        auto map = item.first;

        for (auto iter = map.begin(); iter != map.end(); iter++)
        {
            if ('Z' != iter->second)
            {
                QCERR("Bad pauliZ Hamiltonian");
                throw std::string("Bad pauliZ Hamiltonian.");
            }

            tmp_vec.push_back(qubit_vec[iter->first]);
        }

        if (!tmp_vec.empty())
        {
            circuit.insert(simulateZTerm(tmp_vec, item.second, t));
        }
    }

    return circuit;
}

int main()
{
    PauliOperator op = getHamiltonian();

    QuantumMachine *machine = initQuantumMachine();
    QVec qlist;
    for (int i = 0; i < op.getMaxIndex(); ++i)
        qlist.push_back(machine->qAlloc());

    VQC vqc;
    for_each(qlist.begin(), qlist.end(), [&vqc](Qubit* qbit)
    {
        vqc.insert(VQG_H(qbit));
    });

    int qaoa_step = 4;

    var x(MatrixXd::Random(2 * qaoa_step, 1), true);

    for (auto i = 0u; i < 2*qaoa_step; i+=2)
    {
        vqc.insert(simulatePauliZHamiltonian(qlist, op.toHamiltonian(), x[i + 1]));
        for (auto _q : qlist) {
            vqc.insert(VQG_RX(_q, x[i]));
        }
    }

    var loss = qop(vqc, op, machine, qlist);
    auto optimizer = MomentumOptimizer::minimize(loss, 0.02, 0.9);

    auto leaves = optimizer->get_variables();
    constexpr size_t iterations = 100;
    for (auto i = 0u; i < iterations; i++)
    {
        optimizer->run(leaves);
        std::cout << " iter: " << i << " loss : " << optimizer->get_loss() << std::endl;
    }

    QProg prog;
    QCircuit circuit = vqc.feed();
    prog << circuit;

    directlyRun(prog);
    auto result = quickMeasure(qlist, 100);

    for (auto i:result)
    {
        std::cout << i.first << " : " << i.second << " ";
    }

    return 0;
}

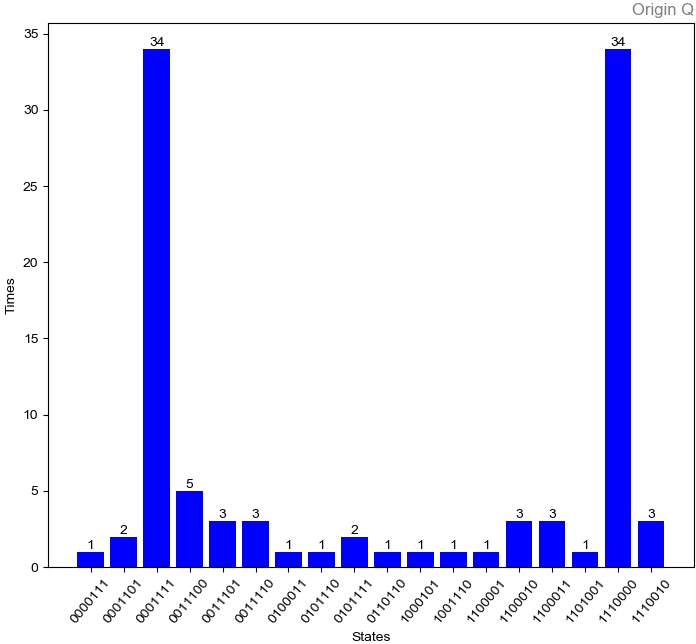
我们将测量的结果绘制出柱状图，可以看到'0001111'和'1110000'这两个比特串测量得到的概率最大，也正是我们这个问题的解。