HHL算法

HHL算法是一种求解线性方程组的量子算法，线性方程组在许多领域中都有着广泛的实际应用。

问题背景概述

线性方程组问题可定义为： 给定矩阵 \(A\in C^{N\times N}\) 和向量 \(\vec{b}\in C^N\) ，找到 \(\vec{x}\in C^N\) 满足 \(A\vec{x}=\vec{b}\)。

如果矩阵A每行或每列最多具有s个非零元，则将线性方程组称为s-稀疏线性方程组。用经典算法（共轭梯度法）来解决N维的s-稀疏线性方程组，需要的时间复杂度为 \(O\left(Nsk\log{\left(\frac{1}{\varepsilon}\right)}\right)\)，这里k表示系统的条件数， \(\varepsilon\) 表示近似的精度。HHL是一种量子算法，当A是自共轭矩阵时，用HHL算法解线性方程组的时间复杂度为 \(O\left(\log{\left(N\right)}s^2\frac{k^2}{\varepsilon}\right)\)。

HHL算法相对于经典算法有着指数级的加速，但经典算法可以返回精确解，而HHL算法只能返回近似解。

注解

HHL算法是一种纯量子算法，它和它的改进版的出现对于证明量子算法的实用性有着重大意义。

算法原理

在对线性方程组进行一定格式转换后可以以HHL算法进行求解，HHL算法主要包含了以下三大步骤，并需要使用右端项比特、存储比特和辅助比特总共三个寄存器。

  1. 构造右端项量子态，对存储比特及右端项比特进行参数含左端项矩阵的相位估计，将左端项矩阵的整数形式特征值全部转移到存储比特的基向量中。
  2. 进行一系列参数含特征值的受控旋转，过滤出所有的特征值相关量子态，将特征值从存储比特的基向量转移到振幅；
  3. 对特征存储比特及右端项比特进行逆相位估计，将存储比特振幅上的特征值合并到右端项比特上，当辅助比特测量得到特定状态时，在右端项比特上可得到解的量子态。

在进行算法具体步骤之前，需要对经典形式的线性方程组求解问题 \(A\vec{x}=\vec{b}\) 进行特定转换：

不失一般性地假设矩阵 \(A\) 为自共轭矩阵，否则取

\[\begin{split}\begin{aligned} C_A=\left[\begin{matrix}0&A\\A^H&0\\\end{matrix}\right], C_b=\left[\begin{matrix}b\\0\\\end{matrix}\right], C_x=\left[\begin{matrix}0\\x\\\end{matrix}\right], \end{aligned}\end{split}\]

使得 \(C_A\vec{C_x}=\vec{C_b}\) 成立且满足 \(C_A\) 自共轭。

以下内容中将默认A为自共轭矩阵。

将向量 \(\vec{b},\vec{x}\) 分别归一化后采用编码到振幅上的方式映射到量子态 \(\left|b\right\rangle,\left|x\right\rangle\) ，原问题转换为 \(A\left|x\right\rangle=\left|b\right\rangle\).

对矩阵 \(A\) 进行谱分解有

\[\begin{aligned} A=\sum_{j=0}^{N-1}\lambda_j\left|u_j\right\rangle\left\langle u_j\right|,\lambda_j\in R. \end{aligned}\]

其中 \({{\lambda}_j,u_j}\) 为矩阵A的特征对（特征值及相应的特征向量）。

将 \(\left|b\right\rangle\) 以特征向量基展开，得到

\[\begin{aligned} \left|b\right\rangle=\sum_{j=0}^{N-1}{b_j\left|u_j\right\rangle},b_j\in C. \end{aligned}\]

于是原方程组的解可表示为

\[\left|x\right\rangle=A^{-1}\left|b\right\rangle=\sum_{j=0}^{N-1}{\lambda_j^{-1}b_j\left|u_j\right\rangle.}\]

显而易见算法的基本思路应当是从右端项量子态 \(\left|b\right\rangle\) 出发构造解量子态 \(\left|x\right\rangle\) 。

通过QPE提取特征值

为了将矩阵 \(A\) 的特征值提取到解量子态的振幅，首先需要完成特征值的提取。 由前文可知，QPE量子线路可以用于特征值提取。

对 \(\left|0\right\rangle^{\otimes n}\left|b\right\rangle\) 进行一次QPE操作，得到

\[\begin{aligned} {QPE(\left|0\right\rangle}^{\otimes n}\left|b\right\rangle)=\sum_{j=0}^{N-1}{b_j\left|\widetilde{\lambda_j}\right\rangle\left|u_j\right\rangle}. \end{aligned}\]

其中 \(\widetilde{\lambda_j}\) 是对应特征值 \(\lambda_j\) 的近似整数，细节参见QPE部分介绍。 于是矩阵A的特征值信息存入到了基向量 \(\left|\widetilde{\lambda_j}\right\rangle\) 中。

通过受控旋转转移特征值

构造如下受控旋转 \(CR(k)\)

\[\begin{split}\begin{aligned} CR(k)(\left|a\right\rangle\left|j\right\rangle)=\left\{\begin{matrix} RY(2\arcsin{\frac{C}{k}})\left|a\right\rangle\left|k\right\rangle,j=k,\\ \left|a\right\rangle\left|j\right\rangle,j\neq k, \end{matrix}\right. \end{aligned}\end{split}\]

式中 \(C\) 为 \(\widetilde{\lambda_j}\) 的归一化系数，有 \(C\le\smash{\displaystyle\min_{j}} {\left|\widetilde{\lambda_j}\right|}\)从而任意 \(\frac{C^2}{{\widetilde{\lambda_j}}^2}\le 1\)。对 \(\sum_{j=0}^{N-1}{b_j\left|0\right\rangle \left|\widetilde{\lambda_j}\right\rangle\left|u_j\right\rangle}\) 经过遍历式旋转量子门操作后可以得到

\[\begin{aligned} (\prod (CR(k)\otimes I))\sum^{N-1}_{j=0}b_j\left|0\right\rangle\left|\widetilde{\lambda_j}\right\rangle \left|u_j\right\rangle=\sum_{j=0}^{N-1}{(\sqrt{1-\frac{C^2}{{\widetilde{\lambda_j}}^2}}\left|0\right\rangle +\frac{C}{\widetilde{\lambda_j}}\left|1\right\rangle)b_j\left|\widetilde{\lambda_j}\right\rangle\left|u_j\right\rangle}. \end{aligned}\]

通过逆QPE输出结果量子态

理论上，受控旋转后的量子态已经可以通过测量得到解量子态 \(\left|x\right\rangle\) 。

但为了避免出现 \(\left|u_j\right\rangle\) 相同但\(\left|\widetilde{\lambda_j}\right\rangle\) 不同的需要合并的量子态\(\frac{C }{\widetilde{\lambda_j}}b_j\left|1\right\rangle\left|\widetilde{\lambda_j}\right\rangle\left|u_j\right\rangle\)，应当选择逆QPE操作来得到形如 \(\frac{C }{\widetilde{\lambda_j}}b_j\left|1\right\rangle\left|0\right\rangle\left|u_j\right\rangle\) 的结果量子态。

对旋转结果进行逆QPE，有

\[\begin{split}\begin{aligned} & (I\otimes{QPE}^{\dagger})\sum_{j=0}^{N-1}{(\sqrt{1-\frac{C^2}{{\widetilde{\lambda_j}}^2}}\left|0\right\rangle+\frac{C}{\widetilde{\lambda_j}} \left|1\right\rangle)b_j\left|\widetilde{\lambda_j}\right\rangle\left|u_j\right\rangle} \\ & =\sum_{j=0}^{N-1}{(b_j}\sqrt{1-\frac{C^2}{{\widetilde{\lambda_j}}^2}}\left|0\right\rangle\left|0\right\rangle\left|u_j\right\rangle+b_j \frac{C}{\widetilde{\lambda_j}}\left|1\right\rangle\left|0\right\rangle\left|u_j\right\rangle). \end{aligned}\end{split}\]

事实上即使是这种形式的结果量子态，由于误差的存在，依然无法在第一个和第二个量子寄存器分别为 \(\left|1\right\rangle,\left|0\right\rangle\) 的情况下以概率1得到解量子态 \(\left|x\right\rangle=\sum_{j=0}^{N-1}{\lambda_j^{-1}b_j\left|u_j\right\rangle}\) 。

注解

HHL算法充分利用了量子相位估计提取特征值信息的功能，巧妙构造了受控旋转门从存储比特的基向量中抓取特征值存入振幅， 最后利用逆相位估计还原存储量子比特，从而得到了振幅含特征值的方程解。

量子线路图与参考代码

HHL算法的量子线路图如下所示

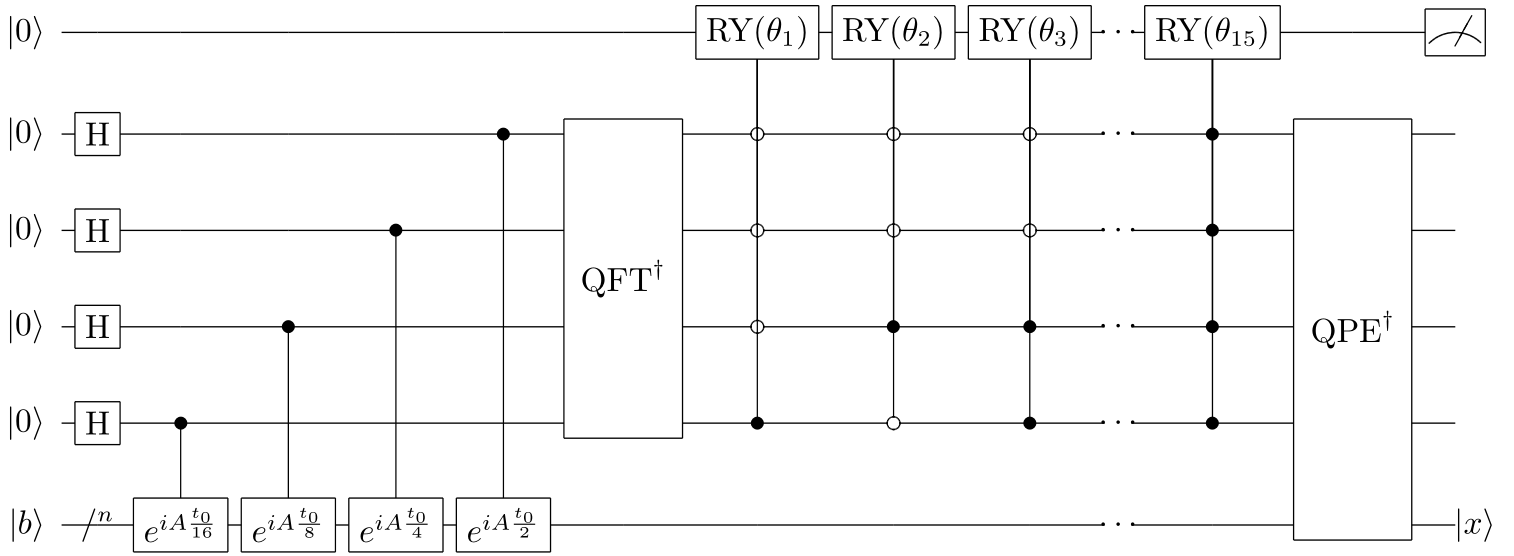
_images/HHL_Alg.png

基于QPanda-2.0的HHL算法实现代码较为冗长，此处不作详述，此处仅介绍QPanda-2.0中提供的几个HHL算法调用接口。

QCircuit build_HHL_circuit(const QStat& A, const std::vector<double>& b, QuantumMachine *qvm, const uint32_t precision_cnt = 0);
QStat HHL_solve_linear_equations(const QStat& A, const std::vector<double>& b, const uint32_t precision_cnt = 0);

第一个函数接口用于得到HHL算法对应的量子线路，第二个函数接口则可以输入QStat格式的矩阵和右端项，返还解向量。 目前第一个函数接口返回的线路需要追加特殊后处理，得到的并不是直接求解的结果，一般推荐使用第二个函数接口HHL_solve_linear_equations。

选取 \(A=\bigl(\begin{smallmatrix} 1 & 0 \\ 0 & 1 \\ \end{smallmatrix}\bigr), b=\begin{pmatrix} 0.6,0.8\end{pmatrix}^T\) ， 验证HHL的代码实例如下：

#include "QPanda.h"
#include <Extensions\QAlg\HHL.h>

int main(void)
{
   std::vector<double> b = { 0.6,0.8 };
   QStat A = { 1,0,0,1 };

   auto result = HHL_solve_linear_equations(A, b);
   for (auto& val : result)
   {
   cout << val << endl;
   }
   return 0;
}

输出结果应该和右端项向量一样是 \([0.6,0.8]\)，虚数项参数为0。因为误差会出现较小的扰动：

(0.6,0)
(0.8,0)